Answer:
Option A
Explanation:
We have,
$5x^{2}-xy-5x+y=0$ are normal to circle S=0
$\therefore$ Centre of circle S=0 is point of intersection of line
$5x^{2}-xy-5x+y=0$
(x-1)(5x-y)=0
x=1, 5x-y=0
$\therefore$ Centre (1,5)
Centre of circle S'= $ x^{2}+y^{2}-2x+2y-7=0$ is (1,-1)
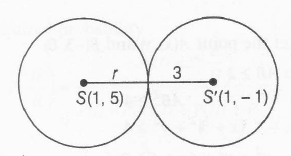
and radius =3
$SS'=\sqrt{(1-1)^{2}+(5+1)^{2}}=6$
$\therefore$ r= SS'-3=6-3=3
Equation of circle
S= $ (x-1)^{2}+(y-5)^{2}= (3)^{2}$
= $x^{2}+y^{2}-2x-10y+17=0$
Equation of chord of contact at (1,-1) to S=0 is
$x-y-2\frac{(x-1)}{2}-10\frac{(y-1)}{2}+17=0$
x-y-x-1-5y+5+17=0
$\Rightarrow$ -6y+21=0
$\Rightarrow$ 2y-7=0
