Discussion Forum



1)

Area of the region (in sq units)  bounded by the curve y =$\sqrt{x}$, x= $\sqrt{y}$ and the lines x=1, x=4 , is 


A) $\frac{8}{3}$

B) $\frac{49}{3}$

C) $\frac{16}{3}$

D) $\frac{14}{3}$

Answer:

Option B

Explanation:

We have ,

  y =$\sqrt{x}$, x= $\sqrt{y}$ ,x=1 ,x=4

The graph  of curves are 

672021216_m1.PNG

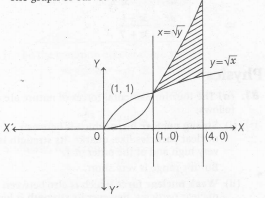
 Area of shaded region

$=\int_{1}^{4} (x^{2}-\sqrt{x})dx=\left[\frac{x^{3}}{3}-\frac{2}{3}(x)^{3/2}\right]_{1}^{4}$

 = $\left(\frac{64}{3}-\frac{16}{3}\right)-\left(\frac{1}{3}-\frac{2}{3}\right)$

 = $\frac{64-16-1+2}{3}=\frac{49}{3}$