Discussion Forum



1)

 In the diode-based rectifier  circuit  given below, If $V_{s}-V_{m}\sin \omega t$ and the diode is ideal, then the average value of $V_{L}$ is 

982021383_m4.PNG


A) $\frac{R_{L}}{(R_{L}+R_{S})}\frac{V_{m}}{\pi}$

B) $R_{L} V_{m} \sin \omega t$

C) $\frac{R_{L}}{(R_{L}+R_{S})}V_{m}$

D) $\frac{R_{L}}{(R_{L}+R_{S})}V_{m} \sin \omega t$

Answer:

Option A

Explanation:

 Given , AC voltage , $V_{s}=V_{m}\sin  \omega t$

and $V_{m}$= maximum value of voltage 

In the given circuit diode will only conduct current in forward bias, so output across $R_{L}$ will be

982021783_m5.PNG

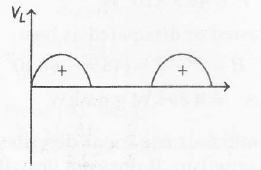
 Average Voltage , $V_{av}=\frac{V_{m}}{\pi}$

average current $I_{av}= \frac{V_{av}}{R}$

 Total resistance  , $R= R_{S}+R_{L}$

 $I_{av}=\frac{V_{m}}{(R_{S}+R_{L})\pi}$

Now, voltage across $R_{L}$

 $V_{L}=I_{av}.R_{L}$

$V_{L}$= $\frac{R_{L}}{(R_{L}+R_{S})}\frac{V_{m}}{\pi}$