Discussion Forum

A small object  is thrown at an angle $45^{0}$ to the horizontal with an initial velocity $v_{0}$ .The velocity is averaged for first $\sqrt{2}$  s  and the magnitude of average velocity comes out to be the same as that of initial velocity,i.e,$ |v_{0}|$. The magnitude $|v_{0}|$ will be  (take ,g=10 m/s²)

Answer:

Explanation:

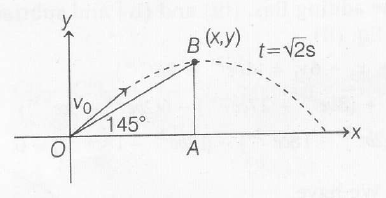
Let object is at B(x,y) after $t=\sqrt{2}s$

Then, $x=u_{x} \times t=v_{0}\cos 45^{0} \times \sqrt{2}=v_{0}$

and $y= u_{y}t-\frac{1}{2}a_{y}t^{2}=v_{0}(\sin 45^{0}) \sqrt{2}-\frac{1}{2}(10)\times  (\sqrt{2})^{2}$

   =$(v_{0}-10)m$

 Displacement OB of particle is

$OB=\sqrt{OA^{2}+AB^{2}}$= $\sqrt{v_{0}^{2}+(v_{0}-10)^{2}}$

So, $v_{avg}= \frac{OB}{t}=v_{0}$  $OB=v_{0}t$

 $\Rightarrow$   $\sqrt{v_{0}^{2}+(v_{0}-10)^2}=v_{0}\sqrt{2}\Rightarrow v_{0}^{2}+(v_{0}-10)^{2}=2v_{0}^{2}$

$\Rightarrow $     $v_{0}-10=\pm v_{0}$         $2v_{0}=10\Rightarrow v_{0}=5 ms^{-1}$