Discussion Forum

 The locus  of the mid-point of the line segment joining the focus to a moving point on the parabola, $y^{2}=4ax$  is a conic . The equation of the directrix of that conic is 

Answer:

Explanation:

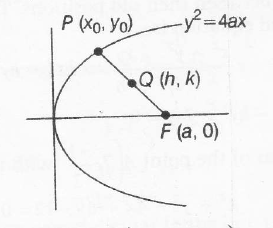
Let Q(h,k)  be the mid-point of the line  joining  the  focus F(a,0)  and variable point $p(x_{0},y_{0})$.

$\therefore$       $(h,k)=\left(\frac{x_{0}+a}{2},\frac{y_{0}}{2}\right)$

$\Rightarrow$     $h=\frac{x_{0}+a}{2}$ and $k=\frac{y_{0}}{2}$

$\Rightarrow$      $x_{0}=2h-a$   and $y_{0}=2k$

Since P(x₀,y₀) lies on parabola $y^{2}=4ax$

 $\therefore$         $y_{0}^{2}=4ax_{0} \Rightarrow (2k)^{2}=4a(2h-a)$

$\Rightarrow$     $4k^{2}=4a(2h-a)\Rightarrow  k^{2}= 2a \left(h- \frac{a}{2}\right)$

Which is equation  of parabola 

$\therefore$   $y^{2}=2a\left(x-\frac{a}{2}\right)$

$\therefore$    Equation of directrix is given by

$x-\frac{a}{2}=\frac{-a}{2}\Rightarrow x=0$