Discussion Forum



1)

 In a quadrilateral  PQRS, A divides SR in the ratio 1:3  and B is the mid-point of PR . If 3SR-QR-3PS-PQ=k AB, then k=


A) 2

B) 4

C) 6

D) 8

Answer:

Option D

Explanation:

Given PQRS a  quadrilateral  A divides SR  in the ratio 1:3 and B is the mid point PR.

 482021641_m6.PNG

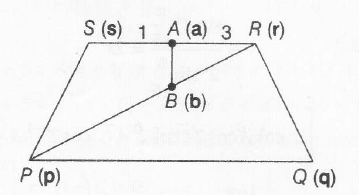
Let the position vector of P,Q, R, S, A , B arep,q,r,s,a and b respectively

$\therefore$    SR=r-s ;QR=r-q             

              PS=s-p, PQ=q-p

AB=b-a

  $a=\frac{3s+r}{4};b=\frac{p+r}{2}$

Now, 3SE-QR-3PS-PQ=KAB

 3(r-s)-(r-q)-3(s-p)-(q-p)=k(b-a)

$\Rightarrow$  3r-3s-r+q-3s+3p-q+p=k

  $\left(\frac{p+r}{2}-\frac{3s+r}{4}\right)$

 $=2r-6s+4p=k\left(\frac{2p+2r-3s-r}{4}\right)$

 $=8r-24s+16p=2kp+2kr-3ks$

$\therefore$  k=8