Discussion Forum

In a $\triangle $ ABC, sin A and sin B satisfy   $c^{2}x^{2}-c(a+b)x+ab=0$ , then 

Answer:

Explanation:

 We have,

  $c^{2}x^{2}-c(a+b)x+ab=0$

$\Rightarrow$   $c^{2}x^{2}-cax-cbx+ab=0$

$\Rightarrow$   $cx(cx-a)-b(cx-a)=0$

$\Rightarrow$  (cx-a)(cx-b)=0

$\Rightarrow$   cx-a=0 or cx-b=0

 $\Rightarrow$        $x=\frac{a}{c}$ and x=$\frac{b}{c}$

 As, sin A and sin B  are roots of the given equation 

Let $\sin A= \frac{a}{c}$  and $\sin B =\frac{b}{c}$

$\Rightarrow$        $c= \frac{a}{\sin A} $  and c=$\frac{b}{\sin B}$

$\Rightarrow$    $\frac{a}{\sin A}=\frac{b}{\sin B}=c$  ...........(i)

Using sine law, $\frac{a}{\sin A}$=$\frac{b}{\sin B}$=$\frac{c}{\sin C}$   .............(ii)

So, $\frac{c}{\sin c}=c $[From eqs.(i) and (ii) ]

$\Rightarrow$     $\sin c= \frac{c}{c}$

$\Rightarrow$    $\ sin C=1$       [$\because  \sin \frac{\pi}{2}=1$]

$\Rightarrow$    $\angle C=\frac{\pi}{2}$

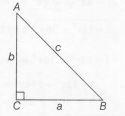
    $\sin A= \frac{a}{c}$ and $\cos A= \frac{b}{c}$

$\therefore$       $\sin A+\cos A= \frac{a}{c}+\frac{b}{c}= \frac{a+b}{c}$