Answer:
Option D
Explanation:
According to question , we can draw the following diagram
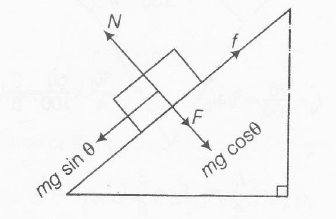
mgsinθ=μ(F+mgcosθ)
F=mgsinθμ−mgcosθ
F=mg[sinθμ−cosθ]
Here,
m=1kg ,g=10 m/s2, θ=300, μ=0.2
F=1×10[sin300.2−cos300]
= 10[12×0.2−√32]
= 10[52−√32]=5[5−√3]
=5[5−1.732]=16.34N