Answer:
Option C
Explanation:
Given , ABCD is a parallelogram with vertices A(4,4,-1), B(5,6,-1), C(6,5,1) and D(x,y,z)
We know that digonals of parallelogram ABCD bisects each other.
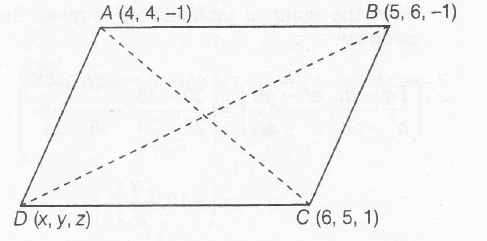
$\therefore$ Mid poinr of Ac= Mid point of BD
$\Rightarrow$ $\left(\frac{4+6}{2},\frac{4+5}{2},\frac{-1+1}{2}\right)=\left(\frac{x+5}{2},\frac{y+6}{2},\frac{z-1}{2}\right)$
$\Rightarrow$ $\left(\frac{10}{2},\frac{9}{2},0\right)=\left(\frac{x+5}{2},\frac{y+6}{2},\frac{z-1}{2}\right)$
On comparing both sides, we get
$\frac{x+5}{2}=\frac{10}{2},\frac{y+6}{2}=\frac{9}{2}$ and $\frac{z-1}{2}=0$
$\Rightarrow$ $x+5=10,y+6=9$ and $z-1=0$
$\Rightarrow$ $x=10-5,y=9-6 $ and z=1
$\Rightarrow$ x=5 ,y=3 and z=1
Thus , D(x,y,z)=D(5,3,1)