Discussion Forum



1)

$f:(-\infty,0] \rightarrow[0,\infty)$ is defined as f(x)=x2 . The domain  and range of its inverse is 


A) Domain$(f^{-1})=[0,\infty)$, Range of $(f^{-1})=(-\infty,0]$

B) Domain$(f^{-1})=[0,\infty)$, Range of $(f^{-1})=(-\infty,\infty]$

C) Domain$(f^{-1})=[0,\infty)$, Range of $(f^{-1})=(0,\infty]$

D) $f^{-1}$ does not exist

Answer:

Option A

Explanation:

We have a function $f:(-\infty,0] \rightarrow [0, \infty)$ defined as f(x)=x2

The graph  of above function is 

 1682021318_m3.PNG

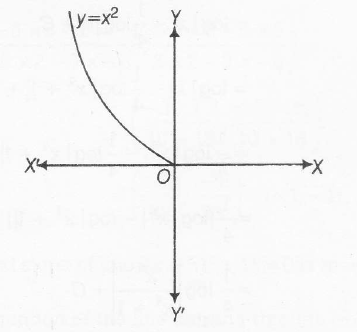
Since, each line parallel to x-axis cuts the above curve at a maximum of one point, therefore f is one-one . Also from the graph it is clear that range $f= (0,\infty)$

$\therefore$     f is onto

 Thus, f is invertible

 

Hence, $f^{-1}:[0, \infty) \rightarrow (-\infty,0]$

$\Rightarrow$    Domain$(f^{-1})=[0,\infty)$,  and Range of $(f^{-1})=(-\infty,0]$