Discussion Forum

The sides of a triangle are in the ratio $1:\sqrt{3}:2$ . Then the  angles are in the ratio

Answer:

Explanation:

We have,

 Ratio of sides of triangle are $1: \sqrt{3}:2$

 Let the sides $k,\sqrt{3}k, 2k,$

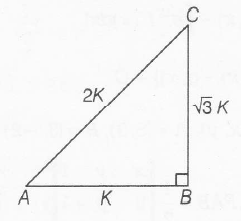
 Since , this triangle is a right angle triangle

 $(2k)^{2}=(\sqrt{3}k)^{2}+(k)^{2}=(2k)^{2}$

 $\therefore$     $\sin A= \frac{\sqrt{3}k}{2k}=\frac{\sqrt{3}}{2}\Rightarrow A=60^{0}$

$\Rightarrow\sin C= \frac{k}{2k}=\frac{1}{2}\Rightarrow C=30^{0}$

 $\Rightarrow$  B=90⁰

 $\therefore$ Ratio of angles are $30^{0}:60^{0}:90^{0}$

$\Rightarrow$   1:2:3