Discussion Forum

A child starts running from rest along a circular track of radius r with constant tangential acceleration a. After a time the feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and ground is 

[ g= acceleration due to gravity]

Answer:

Explanation:

 when a child moves in a circular track, he is acted upon by two forces as shown below.

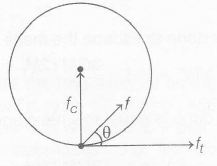
 Here f_c =f sin $\theta$ and f_t= f cos $\theta$,

 As f_c is the centripetal force and f_t= is the tangential force. so

 $f_{c}=\frac{mv^{2}}{r}=f\sin\theta$

 and   $f_{t}= ma= f \cos\theta$

 $\therefore$    Resultant force,   $f_{R}= \sqrt{(f \sin\theta)^{2}+(f\cos\theta)^{2}}$

  $=\sqrt{\left(\frac{mv^{2}}{r}\right)^{2}+(ma)^{2}}$

Also, when the shoes starts slipping  , the friction becomes equal to resultant force.

 $\therefore$      f= f_R

        $\mu mg=\sqrt{\left(\frac{mv^{2}}{r}\right)^{2}+(ma)^{2}}$

 $\mu^{2} m^{2}g^{2}=\frac{m^{2}v^{4}}{r^{2}}+m^{2}a^{2}$         

$\mu^{2}g^{2}=\frac{(at)^{4}+a^{2}r^{2}}{r^{2}}$                   $\left( \because a=\frac{v}{t}\right)$

 or     $\mu^{}=\frac{(a^{4}t^{4}+a^{2}r^{2})^{1/2}}{gr}$