Discussion Forum

 The radius of the circle  passing through the points (5,7),(2,-2) and (-2,0) is

Answer:

Explanation:

 Given, points  (5,7) ,(2,-2) and (-2,0) lie on circle

 Let (h,k) be centre of circle 

$\therefore$    OA=OC

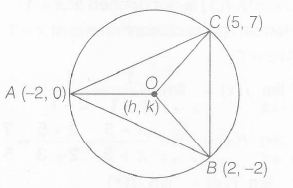
 $\therefore$  $(h+2)^{2}+k^{2}= (h-5)^{2}+(k-7)^{2}$

$\Rightarrow h^{2}+4h+4+k^{2}= h^{2}-10h+25+k^{2}-14k+49$

$\Rightarrow   14h+14k=70$

     h+k=5    .............(i)

 When OA=OB

 $\therefore$   $(h+2)^{2}+k^{2}= (h-2)^{2}+(k+2)^{2}$

 $\Rightarrow h^{2}+4h+4+k^{2}= h^{2}-4h+4+k^{2}+4k+4$

$\Rightarrow 8h-4k=4$

 2h-k=1       .........(ii)

 From eqs. (i) and (ii)  we get

 h=2, k=3

 $\therefore$ Centre of circle (2,3)

 Radius of circle OA=  $\sqrt{(2+2)^{2}+3^{2}}$

  OA=  $\sqrt{4^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5 units$