Answer:
Option A
Explanation:
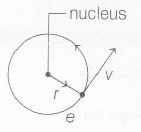
Magnetic moment of revolving electron,
$\mu_{e}=i \times A$
where, i= current and A= area
$\therefore$ $\mu_{e}=\frac{e}{T} \times \pi r^{2}$ (As current, i= $\frac{charge}{time}=\frac{e}{T}$)
where, T= time period of revolution and r= radius of orbit
$\mu_{e}=\frac{e}{2\pi r} \times v \times \pi r^{2}$
( $\because$ Time period (T)= $\frac{ distance }{ speed}$)
where, v= velocity of revolving electron
$\Rightarrow$ $\mu_{e}=\frac{evr}{2} $
Hence, the magnetic moment of revolving electron is $\frac{evr}{2}$