Discussion Forum

P and Q are two  non- zero vectors  inclined to each other at an angle '$\theta$'.'p. and 'q' are unit vectors along P and Q respectively. The   component  of Q in the direction of Q will ve 

Answer:

Explanation:

 Let two vectors P and Q are represented by  graph as below 

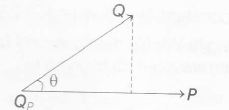
 Here, Q_p  is a vector in the direction of P. Then , from the right angle triangle , we get

$\cos\theta=\frac{Q_{p}}{Q}$     ......(i)

$\Rightarrow$     $ Q_{p}= Q \cos\theta$

 Also,   $\cos\theta=\frac{P.Q}{P Q}\Rightarrow \frac{Q_{p}}{Q}=\frac{P.Q}{P Q}$

$\Rightarrow $   $Q_{p}=\frac{P.Q}{P }$          ......(ii)

 As given that , $\hat{P}$ is the unit vector along P. then

  $\hat{P}=\frac{\underline{P}}{P}$   .......(ii)

 Putting the value of P from Eq.(iii) to Eq. (ii) , we get

  $Q_{p}=\hat{P}.Q$