Answer:
Option B
Explanation:
Let magnetic field at P1 is B1 and at P2 is B2
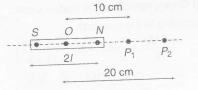
∴ B1B2=x1(x21−l2)2x2(x22−l2)2=(x22−l2)2(x21−l2)2×x1x2
⇒ 252=1020[x22−l2x21−l2]2
or [x22−l2x21−l2]=5
or x22−l2=5x21−5l2
or 4l2=5x21−5x22
= 5 x (10)2-(20)2
= 500-400=100
⇒ l2=25
⇒ l=5 cm
∴ 2l=10 cm