Discussion Forum

$\triangle$ ABC  has vertices at A=(2,3,5), B=(-1,3,2) and C= ($\lambda$,5, $\mu$). If the median through A is equally inclined to the axes, then the values of $\lambda$  and $\mu$  respectively are

Answer:

Explanation:

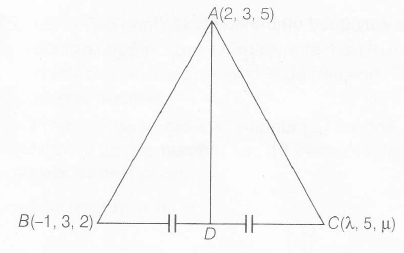
Give , A(2,3,5), B(-1,3,2) and C ($\lambda$,5,$\mu$) be the vertices of $\triangle$ ABC.

Let D be the median through A to BC

=$\left(\frac{\lambda-1}{2},\frac{5+3}{2},\frac{\mu+2}{2}\right)$

=$\left(\frac{\lambda-1}{2},\frac{8}{2},\frac{\mu+2}{2}\right)$

$z=\left(\frac{\lambda-1}{2},4,\frac{\mu+2}{2}\right)$

Now, direction ratio of 

$AD=\left(\frac{\lambda-1}{2}-2,4-3,\frac{\mu+2}{2}-5\right)$

 i.e,  $\left(\frac{\lambda-1-4}{2},1,\frac{\mu+2-10}{2}\right)$

i.e,  $\left(\frac{\lambda-5}{2},1,\frac{\mu-8}{2}\right)$

 Since , the line AD  is equally inclined to the coordinates axes

$\therefore$    $\frac{\lambda-5}{2}=1=\frac{\mu-8}{2}$

 On solving first two, we get

$\frac{\lambda-5}{2}=1$

 $\Rightarrow$      $\lambda$  =7

On solving last two, we get 

     $1=\frac{\mu-8}{2}$

$\Rightarrow$      $\mu$  =10