Discussion Forum

A box contains 6 pens , 2 of which are defective . Two pens are taken randomly  from the box. if r.v.X: number of defective pens obtained , then standard deviation of X= 

Answer:

Explanation:

 Let x be the number of defective pens.

 Two pens are taken randomly from the box,

 $\therefore$     x can take values 0,1,2

  $p(x=0)=\frac{^{4}C_{2}}{^{6}C_{2}}=\frac{4\times3}{6 \times 5}=\frac{2}{5}=\frac{6}{15}$

$p(x=1)=\frac{^{2}C_{1} \times^{4}C_{1}}{^{6}C_{2}}=\frac{2\times4\times2 \times 1}{6 \times 5}=\frac{8}{15}$

$p(x=2)=\frac{^{2}C_{2}}{^{6}C_{2}}=\frac{1\times2\times1 }{6 \times 5}=\frac{1}{15}$

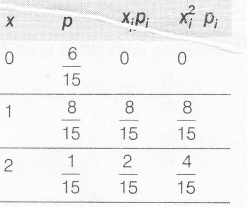
E(x)= $\frac{10}{15}$  and =$\frac {2}{3}$

   E(x² )= $\frac{12}{15}=\frac{4}{5}$

 Standard deviation$=\sqrt{E(x^{2})-[E(x)]^{2}}$

 Standard deviation = $\sqrt{\left(\frac{4}{5}\right)-\left(\frac{2}{3}\right)^{2}}$

    = $\sqrt{\frac{4}{5}-\frac{4}{9}}=\sqrt{\frac{36-20}{45}}$

 $=\sqrt{\frac{16}{45}}=\frac{4}{3\sqrt{5}}$