Answer:
Option B
Explanation:
Let centre of circle on X-axis be (h,0) .The radius of circle will be h
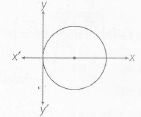
$\therefore$ The equation of circle having centre (h,0) and radius h is
$(x-h)^{2}+(y-0)^{2}=h^{2}$
$\Rightarrow$ $x^{2}+h^{2}-2hx+y^{2}=h^{2}$
$\Rightarrow$ $x^{2}-2hx+y^{2}$=0 ............(i)
On differentiating both sides w.r.t x, we get
$2x-2h+2y \frac{dy}{dx}=0 $ $\Rightarrow$ $h= x+y\frac{dy}{dx}$
On putting h=x+y $\frac{dy}{dx}$ in Eq.(i) , we get
$x^{2}-2\left( x+y \frac{dy}{dx}\right)x+y^{2}=0$
$\Rightarrow$ $-x^{2}+y^{2}-2xy\frac{dy}{dx}=0$
$\Rightarrow$ $(x^{2}-y^{2})+2xy\frac{dy}{dx}=0$