Discussion Forum

1)

In the XY-plane , the region y >0 has a uniform magnetic field $B_{1}\hat{K}$  and the region y<0 has another uniform magnetic field $B_{2}\hat{K}$ . A positively charged particle is projected from origin along the positive Y-axis  with speed $v_{0}=\pi$ms^-1 at t=0, as shown in figure. Neglect gravity in this problem. Let t=T be the time  when the particle crosses the X-axis from below for the first time . If B₂ =4B_1, the average speed of the particle , in ms^-1 , along the  X-axis in the time interval T is........

 

Answer:

Option A

Explanation:

If average speed is considered along X-axis

          $R_{1}=\frac{mv_{0}}{qB_{1}}$ , $R_{2}=\frac{mv_{0}}{qB_{2}}=\frac{mv_{0}}{4qB_{1}}$

                                       $R_{1}>R_{2}$

                     

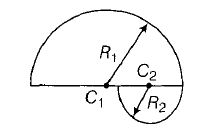
Distance travelled along X-axis 

    $\triangle x=2(R_{1}+R_{2})=\frac{5mv_{0}}{2qB_{1}}$

    Total time = $\frac{T_{1}}{2}+\frac{T_{2}}{2}= \frac{\pi m}{qB_{1}}+\frac{\pi m}{qB_{2}}$

                    $= \frac{\pi m}{qB_{1}}+\frac{\pi m}{4qB_{1}}=\frac{5\pi m}{4qB_{1}}$

   Magnitude of average speed  $= \frac{\frac{5mv_{0}}{2qB_{1}}}{\frac{5\pi m}{4qB_{1}}}$

                                                 = 2m/s