Discussion Forum

1)

A spring  block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0 Nm^-1 and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially ,the spring is in an unstretched condition. Another block of mass 1.0kg moving with a speed of 2.0 ms^-1 collides elastically with the first block. The collision is such that the 2.0kg block does not hit the wall. The distance , in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is...

Answer:

Option A

Explanation:

Just Before Collision

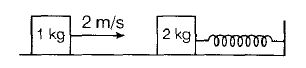
Just After Collision

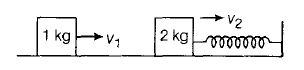
Let velocities of 1 kg and 2 kg blocks just after collision be v₁ and v₂ respectively.

     From momentum conservation principle,

     $1\times 2= 1v_{1}+2v_{2}$       .............(i)

   Collision is elastic. Hence e=1 or relative velocity of separation = relation velocity of approach

               $v_{2}-v_{1}=2$      ..........(ii)

From Eqs.(i) and (ii),

           $v_{2}=\frac{4}{3}m/s$  , $v_{1}=\frac{-2}{3}m/s$

2 kg block will perform SHM after collision,

         $t=\frac{T}{2}=\pi\sqrt{\frac{m}{k}}=3.14s$

Distance = $\mid v_{1}\mid t=\frac{2}{3}\times 3.14$

         =2.093= 2.093 m