Discussion Forum



1)

Two infinitely long straight wires lie in the xy-plane along the lines x=± R. The wire located at x=± R  carries a constant current I1 and the wire located at x= -R carries a constant cureent I2. A circular loop of radius R  is suspended with its centre at (0,0,√3R) and in a plane  parallel to the xy-plane . This loop carries a constant current I in the clockwise direction as seen from above the loop.The current in the wire taken to be postive , if it is in the +$\hat{j}$- direction . Which of the following statements regarding the magnetic field B is (are) true ?


A) If $l_{1}=l_{2}$, then B cannot be equal to zero at the origin (0,0,0)

B) If $l_{1}\gt0$ and $l_{2}\lt0$ , then B can be equal to zero at the origin (0,0,0)

C) If $l_{1}\lt0$ and $l_{2}\lt0$, then B can be equal to zero at the origin (0,0,0)

D) If $l_{1}=l_{2}$ , then the z-component of the magnetic field at the centre of the loop is $(-\frac{\mu_{0}l}{2R})$

Answer:

Option A,B,D

Explanation:

2282019929_orig.JPG

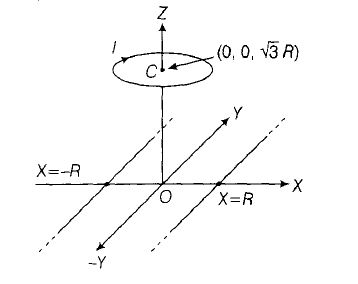
(a)At  origin, B=0 adue to two wires if  l1=l2, hence (Bnet) at origin  is equal to B due to ring. which is non-zero.

(b) If l1 >0 and l2 <0, B at origin due to wires will be along $+\hat{k}$ . Direction of B  due to ring  $-\hat{k}$ direction and hence B can be zero at origin.

(c)  If l1< 0 and l2 > 0, B  at origin due to wires is along $-\hat{k}$ and also along $-\hat{k}$ due to ring, hence B cannot be zero.

(d) 

2282019294_orii.JPG

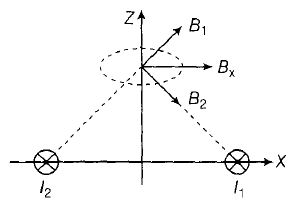
At centre of ring, B due to wires is along x-axis.

       Hence z-component is only because of ring which $B=\frac{\mu_{0}i}{2R}(-\hat{k})$