Discussion Forum

Two batteries with emf 12V and 13V are connected in parallel across a load resistor of 10 Ω . The internal resistances of the two batteries are 1Ω and 2Ω, respectively. The voltage across the load lies between

Answer:

Explanation:

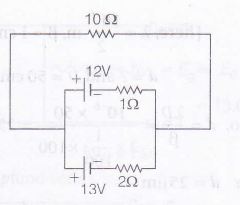
for parallel combination of cells,

$E_{eq}=\frac{\frac{E_{1}}{r_{1}}+\frac{E_{2}}{r_{2}}}{\frac{1}{r_{1}}+\frac{1}{r_{2}}}$

$\therefore$        $E_{eq}=\frac{\frac{12_{}}{1_{}}+\frac{13_{}}{2_{}}}{\frac{1}{1_{}}+\frac{1}{2_{}}}=\frac{37}{2} V$

Potential drop across 10Ω resistance,

  V= ($\frac{E}{R_{total}}$) $\times 10$

    = $\frac{\frac{37}{3}}{(10+\frac{2}{3})}\times 10=11.56 V$

$\therefore$      V= 11.56V

Alternative Method

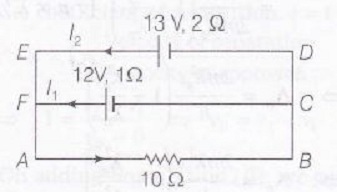
Applying KVL,

in Loop        ABCDFA,

  $-12+10(I_{1}+I_{2})+1\times I_{1}=0$

$\Rightarrow$        $12=11I_{1}-10I_{2}$     .......(i)

Similarly.

in loop ABCDEA,

$-13+10(I_{1}+I_{2})+2\times I_{2}=0$

$\Rightarrow$       $13=10I_{1}+12I_{2}$             ...........(ii)

Solving Eqs. (i) and (ii), we get

$I_{1}=\frac{7}{16}A, I_{2}=\frac{23}{32}A$

 Voltage drop across 10Ω resistance is,

$V=10[\frac{7}{16}+\frac{23}{32}]=11.56V$