Discussion Forum

On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10cm. The resistance of their series combination is 1kΩ. How much was the resistance on the left slot before interchanging the resistances?

Answer:

Explanation:

We have X+Y=1000Ω

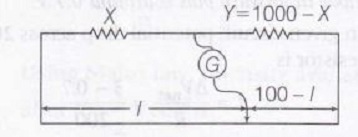
Initially,   $\frac{X}{l}=\frac{1000-X}{100-l}$         ..............(i)

 When X and Y  are interchanged, then

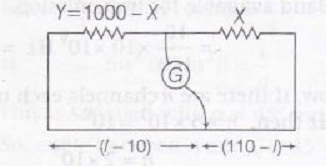
 $\frac{1000-X}{l-10}=\frac{X}{100-(l-10)}$

OR    $\frac{1000-X}{l-10}=\frac{X}{110-l}$        .........(ii)

 From Eqs. (i) and (ii), we get

$\frac{100-l}{l}=\frac{l-10}{110-l}$

$\left(100-l\right)\left(110-l\right)$ = $\left(l-10\right)l$

$11000-100l -110l+l^{2}=l^{2}-10l$

$\Rightarrow$        $11000=200l$

$\therefore$             $l=55 cm$

Substituting the value of l in Eq. (i), we get

$\frac{X}{55}=\frac{1000-55}{100-55}$

$\Rightarrow$          20X=11000

                                 X= 550Ω