Discussion Forum

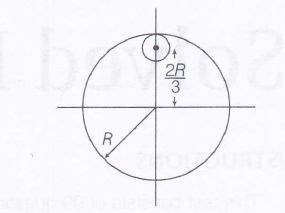
From a unifrom circular disc of radius R and mass 9 M, a small disc of radius $\frac{R}{3}$ is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is

Answer:

Explanation:

Moment of inertia of remaining solid =Moment of intertia of complete solid- Moment of inertia of removed portion

$\therefore$  $I=\frac{9MR^{2}}{2}-[ \frac{M(\frac{R}{3})^{3}}{2} +M(\frac{2R}{2})^{2} ]$

  $\Rightarrow I=4MR^{2}$