Discussion Forum

In a collinear collision, a particle with an initial speed v₀ strikes a stationary particle of the same mass. If the final total kinetic energy is 50% is greater than the  orginal kinetic energy, the magnitude of the relative velocity between the two particles after collision ,is

Answer:

Explanation:

Key idea: Momentum is conserved in all type of collisions,

Final kinectic energy is 50% more than initial kinetic energy

$\Rightarrow\frac{1}{2}mv_{2}^{2}+\frac{1}{2}mv_{1}^{2}\Rightarrow\frac{150}{100}\times\frac{1}{2}mv_{0}^{2}.....(i)$

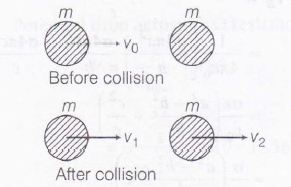
Conservation of momentum gives,

$mv_{0}=mv_{1}+mv_{2}$

$v_{0}=v_{1}+v_{2}......(ii)$

From eq.(i) and (ii), we have

$v_{1}^{2}+v_{2}^{2}+2v_{1}v_{2}=v_{0}^{2}$

$\Rightarrow2v_{1}v_{2}=\frac{-v_{0}^{2}}{2}$

$\therefore (v_{1}^{2}-v_{2}^{2})^{2}=(v_{1}^{2}
+v_{2}^{2})^{2}-4v_{1}v_{2}=2v_{0}^{2}$

or               $v_{rel}=\sqrt{2}v_{0}$