Discussion Forum

Consider two straight lines, each of which is tangent to both the circle x²+ y²=(1/2) and the parabola y² =4x. Let these lines intersect at the point Q. Consider the ellipse whose center ia at the origin O(0,0) and whose semi-major axis is OQ. If the length of the minor  axis of this ellipse is $\sqrt{2}$ , then which of the following statement (s) is (are) TRUE?

Answer:

Explanation:

We  have, Equations of circle

$x^{2}+y^{2}=\frac{1}{2}$

 and equation of parabola

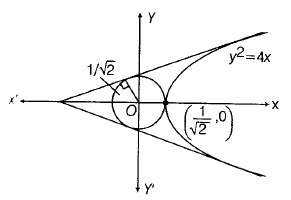
Let the equation of commpn tangent of parabola and circle is

          $y^{}=mx^{}+\frac{1}{m}$

  Since, radius of circle = $\frac{1}{\sqrt{2}}$

               $\frac{1}{\sqrt{2}}$  = $\mid\frac{0+0+\frac{1}{m}}{\sqrt{1+m^{2}}}\mid$

                      = m⁴+m²-m =0

                     = m ± 1

$\therefore$  Equation of common tangents are

                  y=x+1  and y=-x-1

 Intersection point of common tangent at Q(-1,0)

$\therefore$  equation of ellipse

                         $\frac{x^{2}}{1}+\frac{y^{2}}{1/2}=1$

where, a²=1 , b²=1/2

Now,

eccentricity $(e)=\sqrt{1-\frac{b^{2}}{a^{2}}}= \sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}$

and length of latusrectum

               $\frac{2b^{2}}{a}=\frac{2(\frac{1}{2})}{1}=1$

$\therefore$    Area of shadow region

                        = $2\int_{\frac{1}{\sqrt{2}}}^{1} \frac{1}{\sqrt{2}}\sqrt{1-x^{2}}dx$

                        = $\sqrt{2} [\frac{x}{2}\sqrt{1-x^{2}}+\frac{1}{2}\sin^{-1}x]_\frac{1}{\sqrt{2}}^1$

                        = $\sqrt{2}[(0+\frac{\pi}{4})-(\frac{1}{4}+\frac{\pi}{8})]$

                         =    $\sqrt{2}(\frac{\pi}{8}-\frac{1}{4})=\frac{\pi -2}{4\sqrt{2}}$