Discussion Forum



1)

Let T be the line passing through the points P(-2,7) and Q(2,-5). Let F1 be the set of all pairs of circles (S1, S2) such that T is tangent to S1  at P and tangent to S2 at Q , and also such that S1 and S2  touch each other at a point, say M. Let E1 be the set representing  the locus of M as the pair (S1 , S2) varies in F1.  Let the set of all straight line segments joining a pair of distinct points of E1 and passing through the point R(1,1) be F2.  Let E2 be the set of the mid-points of the line segments in the set F2. Then , which of the following statement (s) is (are) TRUE ?


A) The point (-2,7) lies in $E_{1}$

B) The point $(\frac{4}{5},\frac{7}{5})$ does NOT lie in $E_{2}$

C) The point $(\frac{1}{2},1)$ lies in $E_{2}$

D) The point $(0,\frac{3}{2})$ does not lie in $E_{1}$

Answer:

Option A,D

Explanation:

It is given that T is tangents to S1 at P and S2 at Q and S1 and S2 touch externally at M.

 2092019465_rect.JPG

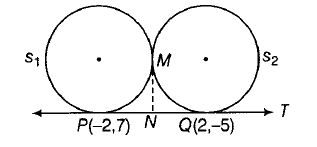
$\therefore$                             MN=NP=NQ

$\therefore$  Locus of M is a circle having PQ as its diameter of circle.

$\therefore$   Equation of circle,  (x-2)(x+2) + (y+5)(y-7)=0

 $\Rightarrow$  x2 +y2-2y-39=0

 Hence, E1 : x2 +y2 -2y-39=0, x≠ ± 2

 Locus of mid-point of chord (h,k) of the circle E1 is xh+yk-(y+k)-39 = h2 +k2 -2k-39

$\Rightarrow$ xh+yk-y-k=h2 +k2 -2k

    Since the chord is passing through (1,1)

           Locus of midpoint of the chord (h,k) is 

                       h+k-1-k= h2 +k2 -2k

$\Rightarrow$   h2 +k2-2k-h+1=0

 Locus is E2 :  x2 +y2 -x-2y+1=0

 Now, after checking options , (a) and (d) are correct.