Answer:
Option D
Explanation:
We have, x2 + y2 =4
Let P(2cosθ,2sinθ) be a point on a circle.
Tangent at P is 2cosθx+2sinθy=4
= xcosθ+ysinθ=2
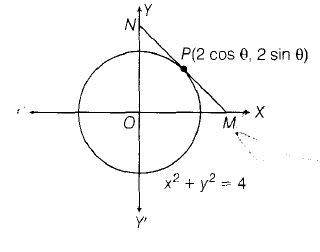
∴ The coordinates at M(2cosθ,0) and N(0,2sinθ)
Let (h,k) is mid-point of MN
∴ h=1cosθ and k=1sinθ
⇒ cosθ=1h and
sinθ=1k
⇒ cos2θ+sin2θ=1h2+1k2
⇒ 1=h2+k2h2.k2
⇒ h2+k2=h2.k2
∴ Mid-point of MN lie on the curve
x2+y2=x2y2