Discussion Forum

Let E₁ E₂ and F₁ F₂ be the chords of S passing through the point P₀ (1,1) and parallel to the X-axis and the Y-axis, respectively. Let G₁ G₂  be the chord of S passing through P₀ and having slope -1. Let the tangents to S at E₁ and E₂ meet at E_3, then tangents to S at F₁ and  F₂ meet at F_3, and the tangents to S at G₁ and G₂  meet at G3. Then, the points E₃, F_3, and G₃ lie on the curve

Answer:

Explanation:

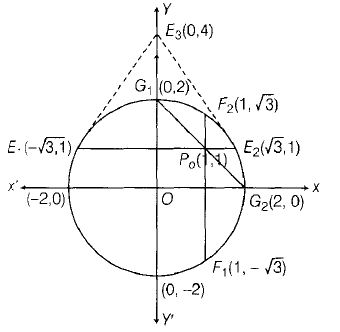
Equation of tangent at E₁ $(-\sqrt{3},1)$ is 

                      $-\sqrt{3}x+y=4$  and at  E₂ $(-\sqrt{3},1)$  is

      $\sqrt{3}x+y=4$

Intersection point of tangent at E₁  and E₂  is (0,4)

            Coordinates of E₃ is (0,4)

Similarly, equation of tangent at F₁ (1,- $\sqrt{3}$)anf F₂ (1, $\sqrt{3}$) are x-$\sqrt{3}$y=4 and  x+$\sqrt{3}$y=4 respectively and intersection point is (4 ,0), i.e. , F₃ (4,0) and equation of tangent at G₁ (0,2) and G₂ (2,0) are 2y=4

and 2x=4, respectively and intersection point is (2,2) ie., G₃ (2,2).

      Point    E₃ (0,4) ,F₃ (4,0)   and  G₃ (2,2)  satisfies the x+y=4.