Answer:
Option C,D
Explanation:
We have
P1: 2x+y-z=3 and
P2 : x+2y+z=2
Here, $\overrightarrow{n_{1}}=\hat{2i}+\hat{j}-\hat{k}$
and $\overrightarrow{n_{2}}=\hat{i}+\hat{2j}+\hat{k}$
(a) Direction ratio of the line of intersection of P1 and P2 is θ $\overrightarrow{n_{1}}\times\overrightarrow{n_{2}}$
i.e
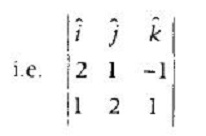
= $(1+2)\hat{i}-(2+1)\hat{j}+(4-1)\hat{k}$
= $3(\hat{i}-\hat{j}+\hat{k})$
Hence, statement a is false
(b) We have
$\frac{3x-4}{9}=\frac{1-3y}{9}=\frac{z}{3}$
$\Rightarrow$ $\frac{x-\frac{4}{3}}{3}=\frac{(y-\frac{1}{3})}{-3}=\frac{z}{3}$
This line is parallel to the line of intersection of P1 and P2 .
Hence statement (b) is false.
(c) Let acute angle between P1 and P2 be θ
We know that ,
$\cos\theta = \frac{\overrightarrow{n_{1} }\overrightarrow{n_{2}}}{\mid\overrightarrow{n_{1}}\mid \mid\overrightarrow{n_{2}}\mid }$
= $\frac{(2\hat{i}+\hat{j}-\hat{k}).(\hat{i}+2\hat{j}+\hat{k})}{\mid 2\hat{i}+\hat{j}-\hat{k}\mid \mid\hat{i}+2\hat{j}+\hat{k}\mid}$
= $\frac{2+2-1}{\sqrt{6}\times\sqrt{6}}= \frac{1}{2}$
θ =60°
Hence the statement (c) is true
(d) Equation of plane passing through the point (4,2,-2) and perpendicular to the line of intersection of P1 and P2
3(x-4)-3(y-2) +3(z+2)=0
$\Rightarrow$ 3x-3y+3z-12+6+6=0
$\Rightarrow$ x-y+z=0
Now distance of the point (2,1,1)
the plane x-y+z=0 is
$D =\mid\frac{2-1+1}{\sqrt{1+1+1}}\mid =\frac{2}{\sqrt{3}}$
Hence statement (d) is true