Discussion Forum



1)

In a Δ PQR , Let  $\angle PQR=30^{0}$ and the side PQ and QR have lengths 10√3 and 10, respectively . Then , which of the following statement (s) is (are) TRUE?


A) $\angle QPR=45^{0}$

B) The area of the $\triangle PQR$ is $25\sqrt{3}$ and $\angle QRP=120^{0}$

C) The radius of the incircle of the $\triangle PQR$ is $10\sqrt{3}-15$

D) The area of the circumcircle of the $\triangle PQR$ is $100\pi$

Answer:

Option B,C,D

Explanation:

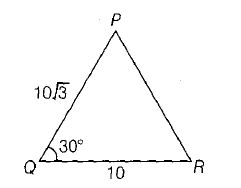
 In  Δ PQR 

          $\angle PQR=30^{0}$

                  PQ = $10\sqrt{3}$    , QR=10

             392019643_new.JPG

By cosine rule

   $\cos 30^{0}=\frac{PQ^{2}+QR^{2}-PR^{2}}{2PQ.QR}$

  $\Rightarrow\frac{\sqrt{3}}{2}=\frac{300^{}+100^{}-PR^{2}}{200\sqrt{3}}$

  $\Rightarrow$     300=300+100-PR2

  $\Rightarrow$     PR=10

   Since , PR=QR= 10

  $\therefore$     $\angle QPR=30^{0}$   and    $\angle QRP=120^{0}$

Area of ΔPQR = $\frac{1}{2}$ PQ.QR $\sin 30^{0}$

              =  $\frac{1}{2}\times10\sqrt{3}\times 10\times\frac{1}{2}=25\sqrt{3}$

Radius of incircle of

            Δ PQR= $\frac{Area of \triangle PQR }{Semi-perimetre of \triangle PQR}$

 i.e   $r=\frac{\triangle }{s}= \frac{25\sqrt{3}}{\frac{10\sqrt{3}+10+10}{2}}=\frac{25\sqrt{3}}{5(\sqrt{3}+2)}$

  $\Rightarrow$       r= $5\sqrt{3}(2-\sqrt{3})=10\sqrt{3}-15$

       and radius of the circumcircle 

                       $(R)=\frac{abc}{4\triangle}= \frac{10\sqrt{3}\times10\times10}{4\times25\sqrt{3}}=10$

$\therefore$   Area of circumcircle of Δ PQR=  $\pi R^{2}=100\pi$

         Hence, option (b), (c) and (d) are correct answer.