Answer:
Option D
Explanation:
Key Idea length ofv projection of the line segment joining a1 and a2 on the plane r .n
= d is $\mid\frac{(a_{2}-a_{1})\times n}{\mid n\mid}\mid$
Length of projection the line segment joining the points (5, -1, 4 ) and (4,-1,3)
on the plane x+y+z = 7 is
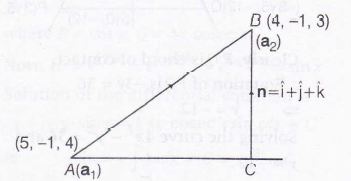
$AC= \mid\frac{(a_{2}-a_{1})\times n}{\mid n\mid}\mid$
$AC= \frac{\mid (-\hat{i}-\hat{k})\times (\hat{i}+\hat{j}+\hat{k)} \mid }{ \mid i+j+k\mid}$
$AC= \frac{\mid \widetilde{i}-\widetilde{k}\mid}{\sqrt{3}}$
$AC= \frac{\sqrt{2}}{\sqrt{3}}$
$AC= \sqrt{\frac{2}{3}}$
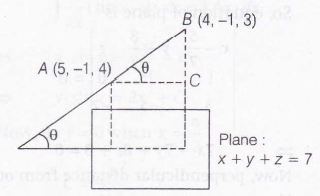
Alternative method
Clearly , DR's of AB are 4-5, -1+1, 3-4,
i.e. -1,0,-1
and DR's of normal to plane are 1,1,1. Now, let θ be the angle between the line and plane , then θ is given by
$ \sin\theta=\frac{\mid -1+0-1\mid}{\sqrt{(-1)^{2}+(-1)^{2}}\sqrt{1^{2}+1^{2}+1^{2}}}$
$=\frac{2}{\sqrt{2}\sqrt{3}}=\sqrt{\frac{2}{3}}$
$\Rightarrow\sin\theta=\sqrt{\frac{2}{3}}\Rightarrow \cos\theta=\sqrt{1-\sin^{2}\theta}$
= $\sqrt{1-\frac{2}{3}}=\frac{1}{\sqrt{3}}$
Clearly, length of projection
= $AB \cos\theta=\sqrt{2}\frac{1}{\sqrt{3}}$ [ $\therefore AB=\sqrt{2}$]
= $=\sqrt{\frac{2}{3}}$