Discussion Forum

Tangent and normal are drawn at P ( 16,16) on the parabola y²=16x, which intersect the axis  of the parabola at A and B , respectively . If C is centre of the circle through the points P,A and B and $\angle$CPB= θ, then the value of $\tan\theta$ is

Answer:

Explanation:

Equation of tangent and normal to the curve y²=16x at ( 16,-16) is x-2y+16= 0 and 2x+y-48=0 respectively,

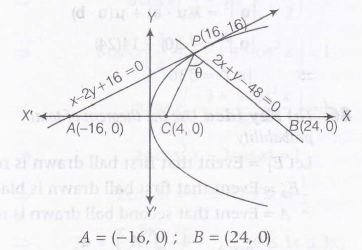
C is the centre of circle passing through PAB

i.e.                C= ( 4,0)

Slope of  $PC= \frac{16-0}{16-4}=\frac{16}{12}=\frac{4}{3}=m_{1}$

Slope of  $PB= \frac{16-0}{16-24}=\frac{16}{-8}=-2=m_{2}$

                               $\tan\theta=\mid \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\mid$

$\Rightarrow$                $\tan\theta=\mid \frac{\frac{4}{3}+2}{1-( \frac{4}{3})( 2)}\mid$

$\Rightarrow$      $\tan\theta=2$