Discussion Forum

A straight line through a fixed point ( 2,3) intersects the coordinate axes at distinct  point P and Q, If O is the origin and the rectangle OPRQ is completed, then the locus of R is 

Answer:

Explanation:

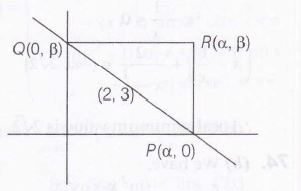
Equation of line PQ is  $\frac{x}{\alpha}+\frac{y}{\beta}=1$

 Since this line is passes through fixed point ( 2,3)

$\therefore$       $\frac{2}{\alpha}+\frac{3}{\beta}=1$

$\therefore$    Locus of R is  $2\beta +3\alpha=\alpha\beta$

i.e.       2y+3x=xy

$\Rightarrow$   3x+2y=xy