Discussion Forum



1)

The radius of a circle having minimum area, which touches the curve y=4-x2 and the line y=|x| , is


A) $2(\sqrt{2}+1)$

B) $2(\sqrt{2}-1)$

C) $4(\sqrt{2}-1)$

D) $4(\sqrt{2}+1)$

Answer:

Option C

Explanation:

Let the radius circle with least area be r

                  Then, then coordinates of centre= (0,4,-r)

      29112019150_circle.PNG

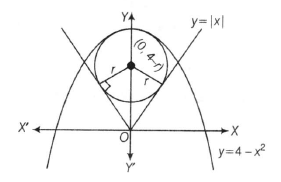
Since, circle touches the line y=x in first quadrant

   $\therefore$    

                        $\mid\frac{0-(4-r)}{\sqrt{2}}\mid=r$

$\Rightarrow$    $r-4=\pm r\sqrt{2}$

$\Rightarrow$         $r=\frac{4}{\sqrt{2}+1}$   or   $\frac{4}{1-\sqrt{2}}$

But                    $r\neq\frac{4}{1-\sqrt{2}}$        $[\because\frac{4}{1-\sqrt{2}}<0]$

  $\therefore$      $r=\frac{4}{\sqrt{2}+1}=4(\sqrt{2}-1)$