Discussion Forum



1)

If the image of the point P(1,-2,3) in the plane 2x+3y-4z+22=0 measured parallel to the line  $\frac{x}{1}=\frac{y}{4}=\frac{z}{5}$ is Q, then PQ is equal to 


A) $3\sqrt{5}$

B) $2\sqrt{42}$

C) $\sqrt{42}$

D) $6\sqrt{5}$

Answer:

Option B

Explanation:

Any line parallel to $\frac{x}{1}=\frac{y}{4}=\frac{z}{5}$ passing through P (1, -2,3) is

     19112019776_auto.PNG

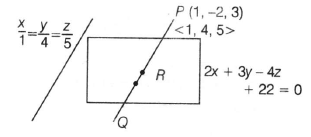
$\frac{x-1}{1}=\frac{y+2}{4}=\frac{z-3}{5} =\lambda (say)$

Any point on above line can be written as (λ +1, 4λ-2, 5λ+3)

 $\therefore$   Coordinates of R are

      (λ +1, 4λ-2, 5λ+3)

Since, point R lies on the above plane 

$\therefore$   2(λ+1)+3(4λ-2)-4(5λ +3) +22=0

    $\Rightarrow$        λ =1

 So, point R is (2,2,8)

  Now, PR=  $\sqrt{(2-1)^{2}+(2+2)^{2}+(8-3)^{2}}$

        =$\sqrt{42}$

  $\therefore$   PQ= 2PR= $2\sqrt{42}$