Discussion Forum

An electric dipole has a fixed dipole moment p, which makes angle θ with respect to X-axis. When subjected to an electric field  $E_{1}=E\hat{i}$ , it experiences a torque $T_{1}=\tau\hat{k}$ . When subjected to another electric field $E_{2}=\sqrt{3}E_{1}\hat{j}$  , it experiences a torque T₂ = -T₁ . The angle θ is 

Answer:

Explanation:

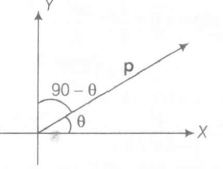
 Torque applied on a dipole $\tau$ =pE sinθ where θ = angle between the axis of the dipole and electric field.

     For electric field $E_{1}=E\hat{i}$

          it means the field is directed along positive X direction, so angle between dipole and field will remain θ , therefore torque in this direction.

        $E_{1}=pE_{1}sin\theta$

  In electric field 

      $E_{2}=\sqrt{3}E\hat{j} $, it means field is directed along positive Y -axis, so angle between dipole and field will 90-θ

  Torque  in this direction

       $T_{2}=pE \sin(90-\theta)$

                $=p\sqrt{3}E_{1}\cos\theta$

According to question

      $\tau_{2}=-\tau_{1}\Rightarrow \mid \tau_{2}\mid =\mid\tau_{1}\mid$

  $\therefore   pE_{1}\sin\theta =p\sqrt{3}E_{1}\cos\theta$

$\tan\theta =\sqrt{3}$

 $\Rightarrow$                   $\tan\theta =\tan 60^{0}$

    θ  = 60^°