Discussion Forum



1)

A uniform magnetic field B exists in the region between x=0 and $x=\frac{3R}{2}$

 (region 2 in the figure)pointing normally into the plane of the paper. A particle with charge +Q and momentum p directed along X-axis enters region 2 from region 1 at point P1(y=-R)

which of the following option(s) is/are correct?

 1012020237_rrrr.PNG


A) when the particle re-enters region 1 through the longest possible path in region 2 the magnitude of the change in its linear momentum between point $P_{1}$ and the farthest point from Y-axis is $\frac{p}{\sqrt{2}}$

B) For $B=\frac{8}{13}\frac{p}{QR}$ , the particle will enter region 3 through the point $P_{2}$ on X-axis

C) For B>$\frac{2}{3}\frac{p}{QR}$ , the particle will re enter region 1

D) For a fixed B, particles of same range Q and same velocity v, the distance between the point $P_{1}$ , and the point of re entry into region 1 is inversely proportional to the mass of the particle

Answer:

Option B,C

Explanation:

a)

1012020205_axis.PNG

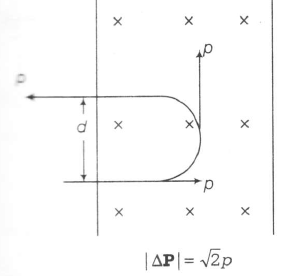
(b)

  r(1-cosθ)=R

   1012020772_QQ.PNG

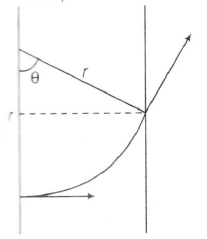
$r\sin\theta =\frac{3R}{2}$

$\frac{\sin\theta}{1-\cos\theta}=\frac{3}{2}$

$\frac{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}{2\sin^{2}\frac{\theta}{2}}=\frac{3}{2}$

$\cot\frac{\theta}{2}=\frac{3}{2}$

$\tan\frac{\theta}{2}=\frac{2}{3}$

$\tan\theta=\frac{2(\frac{2}{3})}{1-\frac{4}{9}}=\frac{\frac{4}{3}}{\frac{5}{9}}=\frac{12}{5}$

1012020644_YYYY.PNG

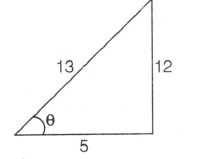
$\sin\theta=\frac{12}{13}$

$r(\frac{12}{13})=\frac{3R}{2}; r=\frac{13R}{8}=\frac{P}{QB};B=\frac{8P}{13QR}$

(c) $\frac{P}{QB}<\frac{3R}{2},B>\frac{2P}{3QR}$

(d)  $r=\frac{mv}{QB},d=2r=\frac{2mv}{QB}\Rightarrow d\propto m$