Discussion Forum



1)

A source of constant voltage V is connected to a resistance R and two ideal inductors L1 and L2 through a switch S as shown. There is no mutual inductance between the two inductors. The switch S is initially open. At t=0, the switch is closed and current begins to flow. Which of the following options is/are correct?

1012020594_Capture.PNG


A) After a long time the current through $L_{1}$ will be $\frac{V}{R}\frac{L_{2}}{L_{1}+L_{2}}$

B) After a long time , the current through $L_{2}$ will be $\frac{V}{R}\frac{L_{1}}{L_{1}+L_{2}}$

C) The ratio of the currents through $L_{1}$ and $L_{2}$ is fixed at all times (t>0)

D) At t=0 the current through the resistance $R is\frac{V}{R}$

Answer:

Option A,B,C

Explanation:

1012020922_res.PNG

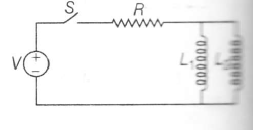
since inductors are connected in parallel

$V_{L_{1}}=V_{L_{2}}$

$L_{1}\frac{dI_{1}}{dt}=L_{2}\frac{dI_{2}}{dt}$

$L_{1}I_{1}=L_{2}I_{2}$

$\frac{I_{1}}{I_{2}}=\frac{L_{2}}{L_{1}}$

Current through resistor  at any time t is given by

$I= \frac{V}{R}(1-e^{-\frac{RT}{L}}) where L=\frac{L_{1}L_{2}}{L_{1}+L_{2}}$

 after log time   $I= \frac{V}{R}$

                    I1 +I2 =I            .........(i)

                    L1I1  = L2I2       ........(ii)

From eq(i) and (ii) , we get

  $I_{1}=\frac{V}{R}\frac{L_{2}}{L_{1}+L_{2}}$,  $I_{2}=\frac{V}{R}\frac{L_{1}}{L_{1}+L_{2}}$

(d) value of current is zero at t=0

value of current V/R at t=∞

 hence option (d) is incorrect