Answer:
Option A,C
Explanation:
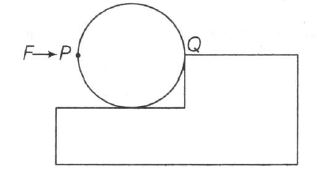
(a) If force is applied normal to surface at P, then the line of action of force will pass from Q and thus τ =0
(b) wheel can climb
(c) τ=F(2Rcosθ)−mgRcosθ
τ∝cosθ
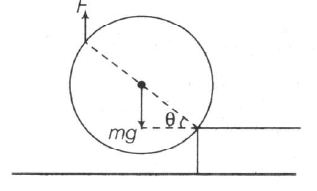
Hence, as θ increases, τ decreases so it correct
(d)
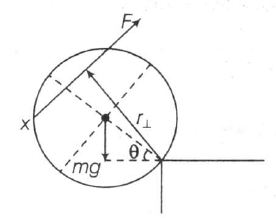
τ=Fr⊥−mgcosθ:τ increases with θ