Answer:
Option A,C,D
Explanation:
when the bar makes an angle of the height of its COM (midpoint) L2cosθ
∴ Displacement
=L−L2sinθ=L2(1−cosθ)
Since, force on COM is only along the vertical direction, Hence COM is falling vertically downwards instantaneous torque about point of contact is
τ=mg×L2sinθ or τ∝sinθ
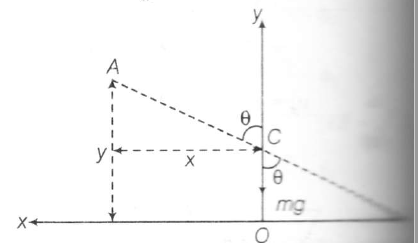
Now,
x=L2sinθ
y=Lcosθ
X2(L2)2+Y2L2=1
Path of A is an ellipse