Discussion Forum



1)

A flat plane is moving normal to its plane through a gas under the action of a constant force F. The gas is kept at very low pressure. The speed of the plane v is much less than the average speed u of the gas molecules. Which of the following options is/are true?


A) At a later time the external force F balances the resistive force

B) The plate will continue to move with constant non-zero acceleration at all times.

C) The resistive force experienced by the plate is proportional to v

D) The pressure difference between the leading and trailing faces of the plate is proportinal to uv

Answer:

Option A,C,D

Explanation:

17122019433_square.PNG

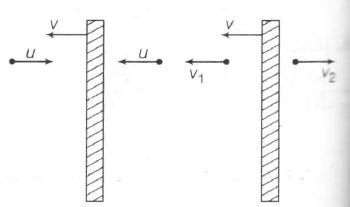
Just before the collision                            Just after the collision

                   $v_{1}=u+2v$

              $\triangle v_{1}=(2u+2v)$

$F_{1}=\frac{\text{d} \rho _{1}}{\text{d}t}$

   =  $ \rho A(u+v)(2u+2v)$

   =  $2 \rho A(u+v)^{2}$

  $v_{2}=(u-2v)$

 $\triangle v_{2}=(2u-2v)$

$  F_{2}=\frac{\text{d} \rho _{2}}{\text{d}t}$

= $  \rho A(u-v)(2u-2v)$

          $=2 \rho A(u-v)^{2}$

17122019920_sqq.PNG

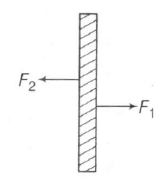
[$\triangle F$   is the net force due to the air molecules on the plate]

      $\triangle F=2 \rho A(4uv)=8 \rho Auv$

    $P= \frac{\triangle F}{A}=8 \rho (uv)$

$F_{net}= (F-\triangle F) =ma$

                         [m is mass of the plate]

   $ F -(8 \rho Au)v=ma $