Discussion Forum



1)

For a linear plot of log (x/ m)versus log p in a Freundlich adsorption isotherm, which of the following statements is correct? (k and n are constants)


A) 1/n appears as the intercept

B) Only 1/n appears as the slope

C) $log\left(\frac{1}{n}\right)$ appears as the intercept

D) Both k and 1/n appear in the slope term

Answer:

Option B

Explanation:

 According to Freundlich adsorption isotherm, $\frac{x}{m}=kp^\frac{1}{n}$

13112020852_5 chemistry.JPG

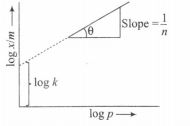
On taking the logarithm of both sides, we get

$\log \frac{x}{m}=\log k + \log p^\frac{1}{n}$

$\log \frac{x}{m}= \log k + \frac{1}{n}\log p$

y=c+mx

$y=\log \frac{x}{m}$ c=intercept = log k

$m= slope=\frac{1}{n}$

 and x= log p