Discussion Forum

If one of the diameters of the circle, given by the equation  $x^{2}+y^{2}-4x+6y-12=0$, is a chord of a circle S, whose centre is at (-3,2), then the radius of S is

Answer:

Explanation:

Given the equation of a circle is  $x^{2}+y^{2}-4x+6y-12=0$, whose centre is (2,-3) and radius

    =$\sqrt{2^{2}+(-3)^{2}+12}=\sqrt{4+9+12}=5$

 Now , according to given information , we have the following figure

   $x^{2}+y^{2}-4x+6y-12=0$

 Clarly, $AO\perp BC$, as O is  mid-point of the  chord

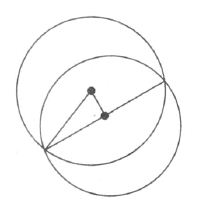
Now, in ΔAOB , we have

$OA=\sqrt{(-3-2)^{2}+(2+3)^{2}}$ 

  $=\sqrt{25+25}=\sqrt{50}=5\sqrt{2}$

and OB=5

   $\therefore  AB= \sqrt{OA^{2}+OB^{2}}$

$\sqrt{50+25}=\sqrt{75}$

  = $5\sqrt{3}$