Discussion Forum

The area (in sq units) of the region ${(x,y):y^{2}\geq2x, and x^{2}+y^{2}\leq 4x, x\geq0, and  y\geq 0}$ is

Answer:

Explanation:

Given the equation  of curve  are

           $y^{2}=2x$   ........(i)

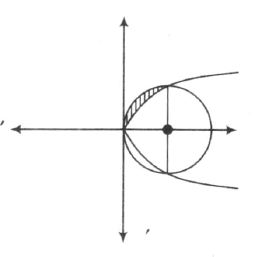
 which is parabola with vertex (0,0) and axis parallel to X-axis

and    x²+y² =4x

 which is circle with centre (2,0) and radius=2                .......(ii)

  on substuting y²=2x in Eq (ii) we get

    x²+2x= 4x

$\Rightarrow x^{2}=2x$

$\Rightarrow x=0$

  or x=2

$\Rightarrow y=0$ or $y=\pm2$   [ using  Eq.. (i)]

Now, the required area is the area of shaded region . ie,

 Required area=  $\frac{Area of a circle}{4}$- $\int_{0}^{2} \sqrt{2x}dx$

$\frac{\pi(2)^{2}}{4}-\sqrt{2}\int_{0}^{2} x^{\frac{1}{2}}dx$

$\pi -\sqrt{2}\left[\frac{x^{\frac{3}{2}}}{{\frac{3}{2}}}\right]_0^2$

$=\pi -\frac{2\sqrt{2}}{3}[2\sqrt{2}-0]$

$=(\pi -\frac{8}{3})$ sq units