Discussion Forum



1)

The region between two concentric spheres of radii a and b, respectively (see the figure), has  volume charge density 

 $\rho =\frac{A}{r}$  where A is a constant and r is distance from the center. At the centre of the spheres is a point charge Q. The value of A, such that the electric field in the region between the sphere will be constant is


A) $\frac{Q}{2\pi a^{2}}$

B) $\frac{Q}{2\pi (b^{2} -a^{2})}$

C) $\frac{2Q}{\pi (a^{2} -b^{2})}$

D) $\frac{2Q}{\pi a^{2} }$

Answer:

Option A

Explanation:

As  E is constant

532020765_process2.JPG

 Hence  , Ea ≡ Eb

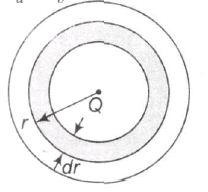
A s per Guass theorem, only Q contributes in electric field

$\therefore    \frac{kQ}{a^{2}}=\frac{k[Q+\int_{a}^{b}4\pi r^{2}dr.\frac{A}{r} }{b^{2}}$

Here,   $k= \frac{1}{4\pi\epsilon_{0}}$

$\Rightarrow Q\frac{b^{2}}{a^{2}}=Q+4\pi A \left[\frac{r^{2}}{2}| _{a}^{b} \right]$

$=Q+4\pi A [\frac{b^{2}-a^{2}}{2}]$

$\Rightarrow  Q (\frac{b^{2}}{a^{2}})=Q+2\pi A (b^{2}-a^{2})$

$\Rightarrow  Q (\frac{b^{2}-a^{2}}{a^{2}})=2\pi A (b^{2}-a^{2})$

$\Rightarrow  A= \frac{Q}{2\pi a^{2}}$