Discussion Forum

Consider a pyramid OPQRS located in the first octant  $ (x\geq 0, y\geq 0,z\geq0)$ with O as origin, and OP and OR along the X-axis and the Y-axis, respectively. The base OPQR of the pyramid is a square with OP=3. The point S is directly above the mid-point T of diagonal OQ such that TS=3Then

Answer:

Explanation:

Given , square base  OP=OR=3

  $\therefore$    P(3,0,0) , R=(0,3,0)

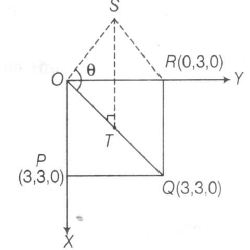
Also, mid-point of OQ is  $T\left(\frac{3}{2},\frac{3}{2},0\right)$

 Since S is directly above the mid-point T of diagonal OQ and ST =3

i.e,  $S\left(\frac{3}{2},\frac{3}{2},3\right)$

Here , DR's of OQ (3,3,0) and DR's of OS   $(\frac{3}{2},\frac{3}{2},3)$

$\therefore\cos \theta=\frac{\frac{9}{2}+\frac{9}{2}}{\sqrt{9+9+0}\sqrt{\frac{9}{4}+\frac{9}{4}+9}}$

$=\frac{9}{\sqrt{18}.\sqrt{\frac{27}{2}}}=\frac{1}{\sqrt{3}}$

$\therefore$ Option (a) is incorrect.

Now, equation of the plane containing the  $\triangle OQS $ is

$\begin{bmatrix}x & y& z \\3 & 3 &0\\3/2 &3/2&3\end{bmatrix}\Rightarrow0\Rightarrow\begin{bmatrix}x &y &z \\1 & 1 &0 \\ 1&1&2\end{bmatrix}=0$

$\Rightarrow  x(2-0)-y(2-0)+z(1-1)=0$

$\Rightarrow  2x-2y=0 $ or x-y=0

$\therefore$ Option  (b) is correct.

 Now, length  of the perpendicular from P(3,0,0) to the plane containing $\triangle OQS $  is 

 $\frac{|3-0|}{\sqrt{1+1}}=\frac{3}{\sqrt{2}}$

 $\therefore$ Option (c)  is correct.

Here, equation of RS is 

 $\frac{x-0}{3/2}=\frac{y-3}{-3/2}=\frac{z-0}{3}=\lambda$

 $\Rightarrow x=\frac{3}{2}\lambda, y=-\frac{3}{2}\lambda+3, z=3\lambda$

 To find the distance from O(0,0) to RS. 

 Let M be the foot of perpendicular.

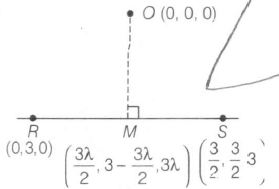
   $\therefore$       $\overline{OM}\perp\overline{RS}\Rightarrow\overline{OM}.\overline{RS}=0$

  $\Rightarrow  \frac{9\lambda}{4}-\frac{3}{2}\left(3-\frac{3\lambda}{2}\right)+3(3\lambda)=0$

$\Rightarrow  $   $\lambda=\frac{1}{3}$

$\therefore$             $M\left(\frac{1}{2},\frac{5}{2},1\right)$

$\Rightarrow  OM=\sqrt{\frac{1}{4}+\frac{25}{4}+1}=\sqrt{\frac{30}{4}}=\sqrt{\frac{15}{2}}$

$\therefore$   Option (d) is correct