Discussion Forum

A solution curve of the differential  equation $(x^{2}+xy+4x+2y+4)\frac{\text{d}y}{\text{d}x}-y^{2}=0$ , x>0, passes through the point (1,3) Then , the solution curve

Answer:

Explanation:

Given, $(x^{2}+xy+4x+2y+4)\frac{\text{d}y}{\text{d}x}-y^{2}=0$

$\Rightarrow$    $[(x^{2}+4x+4)+y(x+2)]\frac{dy}{dx}-y^{2}=0$

$\Rightarrow$    $[(x+2)^{2}+y(x+2)]\frac{dy}{dx}-y^{2}=0$

Put x+2=X  and y=Y, then

$(X^{2}+XY)\frac{dY}{dX}-Y^{2}=0$

$\Rightarrow$     $X^{2}dY+XYdY-Y^{2}dX=0$

$\Rightarrow$    $X^{2}dY+Y(XdY-YdX)=0$

$\Rightarrow$    $-\frac{dY}{Y}=\frac{XdY-YdX}{X^{2}}$

$\Rightarrow$   $-d(\log|Y|)=d(\frac{Y}{X})$

On integrating both sides , we get,

 $-\log|Y|=\frac{Y}{X}+C$

where x+2=X and  y=Y

$\Rightarrow$      $-\log|y|=\frac{Y}{x+2}+C$              ...........(i)

 Since, it passes through the point (1,3)

$\therefore$        $-\log 3 =1+C$

$\Rightarrow$  $C =-1-\log 3$

$=-(\log e +\log 3)$

 $=-\log 3e $

$\therefore$  Eq. (i) becomes

 $\log |y|+\frac{y}{x+2} -\log (3e)=0$

 $\Rightarrow$       $\log\left( \frac{|y|}{3e}\right)+\frac{y}{x+2}=0$       ........(ii)

Now, to check option (a)   y=x+2 intersects the curve.

 $\Rightarrow$     $\log (\frac{|x+2|}{3e})+\frac{x+2}{x+2}=0$

 $\Rightarrow$    $\log (\frac{|x+2|}{3e})=-1$

 $\frac{|x+2|}{3e}=e^{-1}=\frac{1}{e}$  

 $\Rightarrow$   ${|x+2|}=3 $  or  $x+2=\pm3$

 $\therefore$    x=1, -5 (rejected) , as x>0   [given]

 $\therefore$   x=1 only one solution

 Thus ,(a)  is the correct  answer.

To check option (c) we have

 $y=(x+2)^{2}$

and    $\log(\frac{|y|}{3e})+\frac{y}{x+2}=0$

$\Rightarrow$  $\log\left[\frac{|x+2|^{2}}{3e}\right]+\frac{\left(x+2\right)^{2}}{x+2}=0$

$\Rightarrow$   $\log\left[\frac{|x+2|^{2}}{3e}\right]=-\left(x+2\right)$

$\Rightarrow$     $\frac{(x+2)^{2}}{3e}=e^{-(x+2)}$

or     $(x+2)^{2}.e^{x+2}=3e$

$\Rightarrow$   $e^{x+2}=\frac{3e}{(x+2)^{2}}$

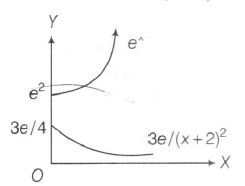
Clearly, they have no solution.

 To check option (d),

$y=(x+3)^{2}$

i.e,      $\log \left[ \frac{|x+3|^{2}}{3e}\right]+\frac{(x+3)^{2}}{(x+2)}=0$

 To check the number of solutions,

  Let  $g(x)= 2\log (x+3)+\frac{(x+3)^{2}}{(x+2)}-\log (3e)$

$\therefore$      $g'(x)=\frac{2}{x+3}+$

$\left( \frac{(x+2).2(x+3)-(x+3)^{2}.1}{(x+2)^{2}}\right)-0$

 $=\frac{2}{x+3}+\frac{(x+3)(x+1)}{(x+2)^{2}}$

Clearly, when x>0, then  ,g' (x)>0

$\therefore$    g(x) is increasing , when x>0

Thus ,when x.0, then g(x) >g(0)

$g(x)>\log (\frac{3}{e})+\frac{9}{4}>0$

Hence, there is no solution

Thus, option  (d) is true