Discussion Forum

1)

Let  $F_{1}(x_{1},0)$ and $F_{2}(x_{2},0)$  , for  $x_{1}<0$ and $x_{2}>0$ , be the foci of the ellipise $\frac{x^{2}}{9}+\frac{y^{2}}{8}=1$ . Suppose a parabola  having vertex at the origin and focus at $F_{2}$ intersects the  ellipse  at the point M in the first quadrant and at point N  in the fourth quadrant

If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the X-axis at Q, then the ratio of area of $\triangle MQR$ to area of the quadrilateral   $MF_{1}NF_{2}$ is

Answer:

Option C

Explanation:

Equation of tangent at $M(3/2,\sqrt{6})$ to     $\frac{x^{2}}{9}+\frac{y^{2}}{8}=1$ is

    $\frac{3}{2}.\frac{x}{9}+\sqrt{6}.\frac{y}{8}=1$                 .........(i)

 which intersect X-axis at (6,0)

   Also, equation of tangent at $N(3/2. -\sqrt{6})$ is

  $\frac{3}{2}.\frac{x}{9}-\sqrt{6}.\frac{y}{8}=1$          ...........(ii)

Eqs. (i) and (ii) intersect on X-axis at R (6.0)                        ..........(iii)

Also normal at  $M(3/2. \sqrt{6})$ is

$Y-\sqrt{6}=-\frac{\sqrt{6}}{2}(x-\frac{3}{2})$

 On solving with y=0,

   we get $Q(\frac{7}{2},0$    ............(iv)

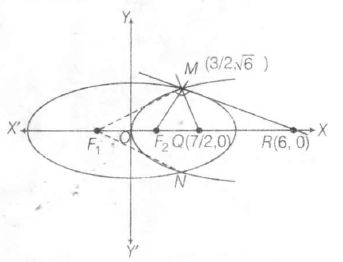
$\therefore$     Area of  $\triangle MQR=\frac{1}{2}(6-\frac{7}{2})\sqrt{6}=\frac{5\sqrt{6}}{4}$ sq units

and area of quadrilateral  $MF_{1}NF_{2}$

              $=2\times\frac{1}{2}[1-(-1)]\sqrt{6}=2\sqrt{6}$ sq units

$\therefore$  Area of  $\triangle MQR$ / Area of quadrilateral  $MF_{1}NF_{2}$    = $\frac{5}{8}$